MDC / MMC

DIVISORES NATURAIS de um número n


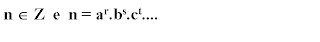
com a, b, c primos e com r, s, t pertencentes aos naturais, temos que o número de divisores naturais de n será dado por:
nD(n)=(r+1).(s+1).(t+1)...

Exemplo:



Como verificamos que os números 1, 2, 3, 4, 6 e 12, dividem 12, logo o número de divisores de 12 é 6.

MDC - Màximo Divisor Comum.

Quando fatoramos dois números, como o exemplo abaixo, verificamos que eles possuem divisores em comum:



Notamos que o maior divisor comum entre 24 e 30 é o número 6.(MDC(24,30)=6)

Mas, quando se trata de números maiores, fica difícil encontrar o máximo divisor em comum por simples fatoração, para tanto existe um algorítimo mais prático, vamos dar um exemplo encontrando o MDC(38,24):

Primeiro constuímos uma grade com três linhas e adicionamos as colunas conforme a necessidade. A primeira linha será do quociente, a segunda do dividendo/divisor e a terceira do resto.

Colocamos inicialmente o número maior (dividendo) depois o menor como (divisor),

Procedendo a divisão colocamos o quociente acima do 24 e o resto abaixo do 38.

Agora o dividendo será o 24 e o o resto anterior será o divisor, por isso repetimos o 14 ao lado do 24 e o quociente colocamos acima do número 14.

O novo resto é 10, colocamos este resto ao lado do número 14 e procedemos a divisão.


Uma nova divisão com resto anterior (4) como divisor

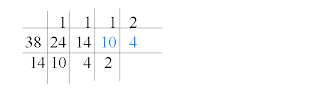
Finalmente a última divisão com resto igual a zero.

Como o número 2 foi o último resto a ser usado como divisor, ele é o divisor comum a 24 e 38 é 2.

MMC - Mínimo Múltiplo Comum.

Para obter o MMC entre dois ou mais números, fatoramos os mesmos simultâneamente, dividindo-os pelo menor fator primo possível.


Logo o mínimo múltiplo comum entre 24 e 38 é 456, ou seja MMC(24,38 ) = 456

É possível obter o MMC e o MDC com o mesmo algoritmo e ao mesmo tempo, bastando para isso assinalar os primos que dividem simultaneamente todos os valores em questão. Teremos:


MMC(24,38)= 456 e MDC(24,38) = 2

Verificamos que nesse caso o número assinalado foi o 2, como mostrado no exemplo do MDC ele é o máximo divisor comum entre 24 e 38. Se houvesse dois ou mais números assinalados, o MDC seria o produto desses números. Veja o próximo exemplo:

MMC(36,24,84)=504 e MDC(36,24,84)= 2.2.3=12

PROPRIEDADE

MDC(a,b).MMC(a,b)= a.b